Категория: Геодезия
GeoMap v1.1.0
В GeoMap версия 1.1.0 е налична нова функционалност за добавяне на точки от текстови файлове (*.txt).
Файловете трябва да се поставят в директория Download/GeoMap на вашето устройство.
Пример: sdcard/Download/GeoMap/rgo-sofia.txt
Структурата на файловете трябва да бъде следната:
pnt,latitude,longitude,elevation,description
където:
- pnt – номер на точка;
- latitude – географска ширина в десетични градуси;
- longitude – географска дължина в десетични градуси;
- elevation – надморска височина;
- description – описание.
Пример за един запис:
pt100,42.50,24.75,500.000,new point
Всички полета са задължителни!
Всеки запис на точка трябва да бъде на нов ред.
За разделител трябва да се използва символа „,“ (запетая).
Видео:
https://youtu.be/Ln_C0vugk0w
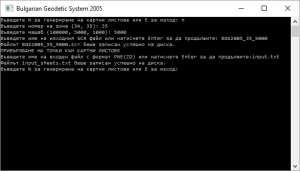
Тестовете гарантират коректно изпълнение на програмата при изчисление координатите на картните листове и определяне на номерата им.
Хранилище на проекта в GitHub:
https://github.com/Nanich87/BGS-2005-Map-Sheets-Generator
Unit тестове:
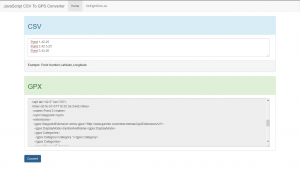
Сорс кодът на JavaScript CSV To GPX Converter може да бъде намерен на следния адрес: github.com/Nanich87/JavaScript-CSV-To-GPX-Converter
Описание:
DPI Converter е безплатна програма за конвертиране на файлове с данни от полски измервания в DPI формат.
Програмата поддържа следните входни формати:
- Topcon LandXML
- Trimble JobXML
- Sokkia SDR33
Във версия 0.7.3 е добавена възможност за връзка чрез сериен порт с различни устройства, поддържащи този порт.
Начален екран:
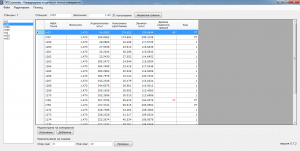
Връзка:
Проект за конвертиране на различни геодезически файлове (KPT, DINI, DPI, KOR, CAD) във универсални формати като TXT, XML, JSON и KML.
Проектът е с отворен код и е достъпен на адрес https://github.com/Nanich87/Survey-Format-Conversion-Factory
Програма за изравнение на планови мрежи
Изравнение на планови мрежи по метода на най-малките квадрати.
Изравнение на засечки – ъглови, линейни, ъглово-линейни, геодезически мрежи, полигони.
Въвеждане на измервания и координати
Изчисляване на ориентировъчните ъгли на дадените точки
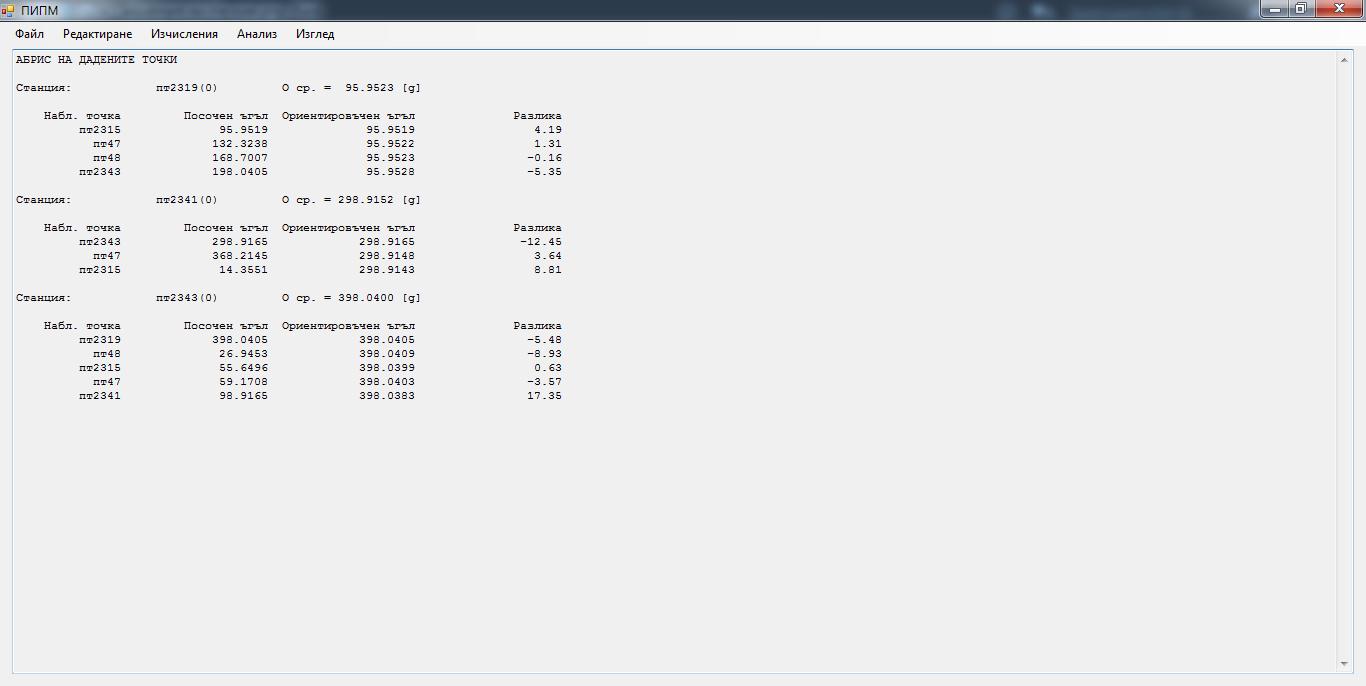
Изчисляване на несъвпаденията в триъгълниците
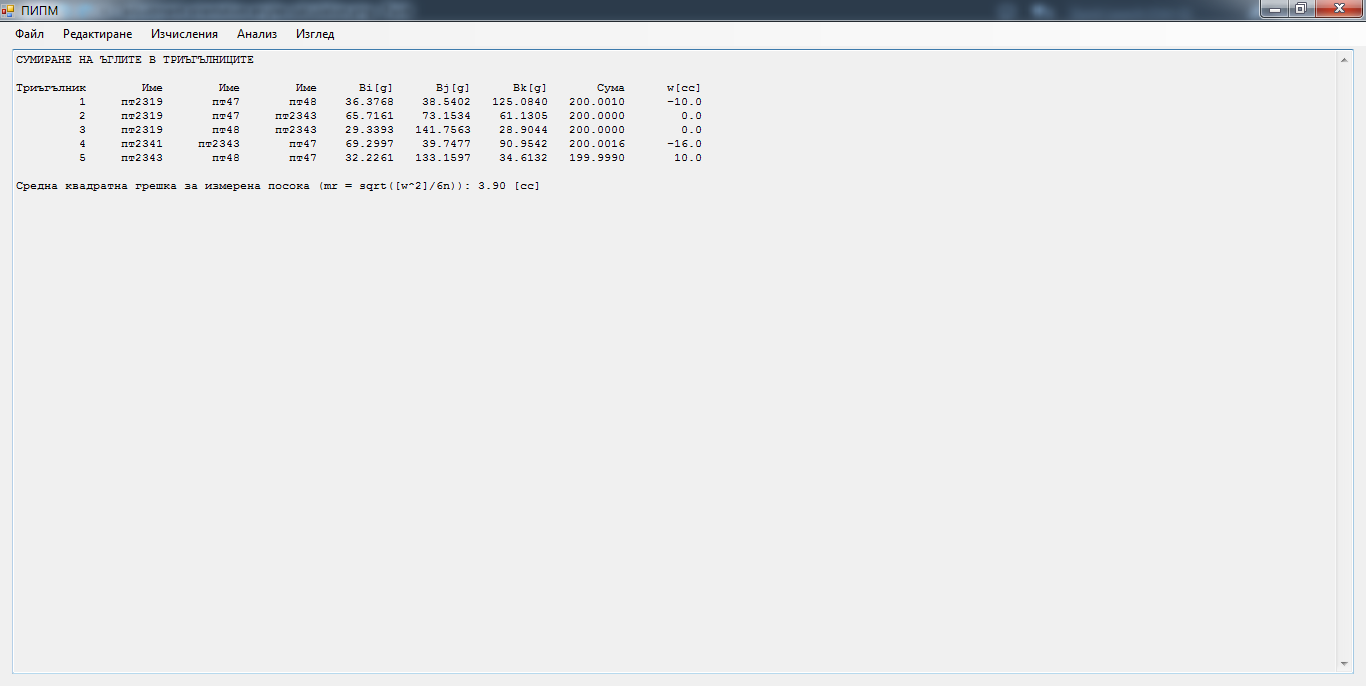
Изчисляване на приблизителни координати на новите точки
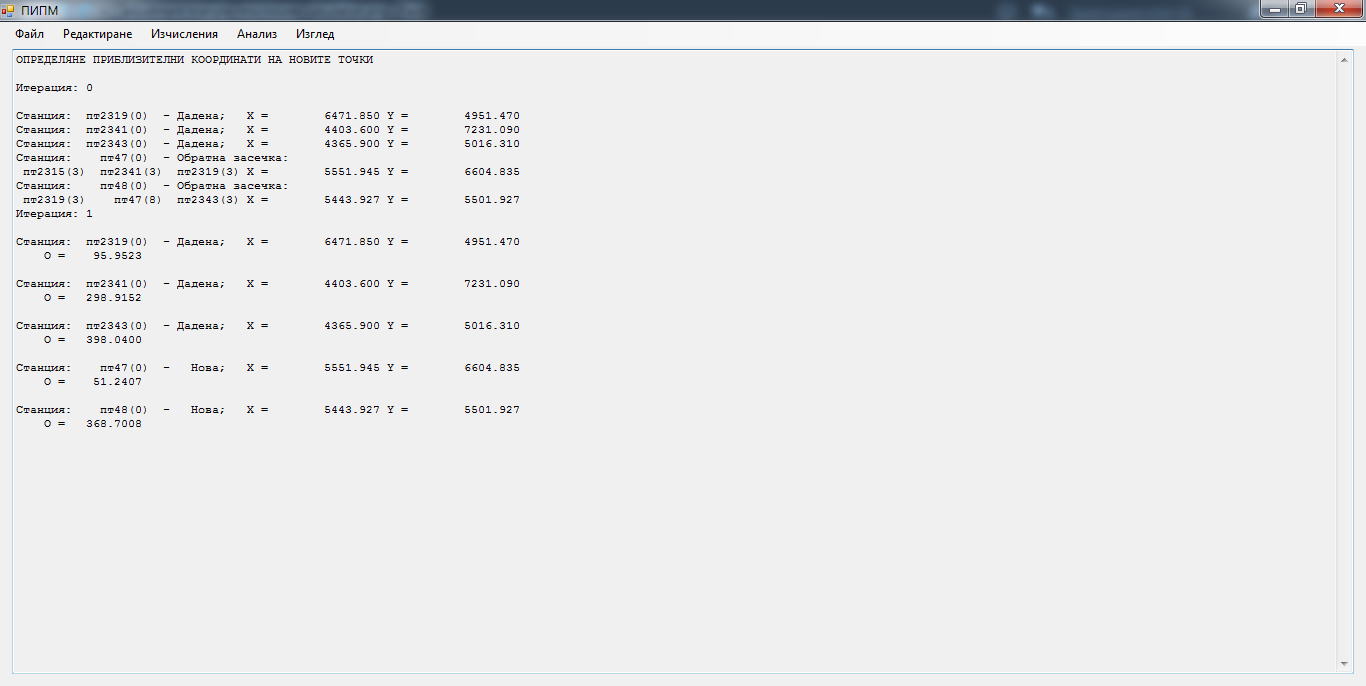
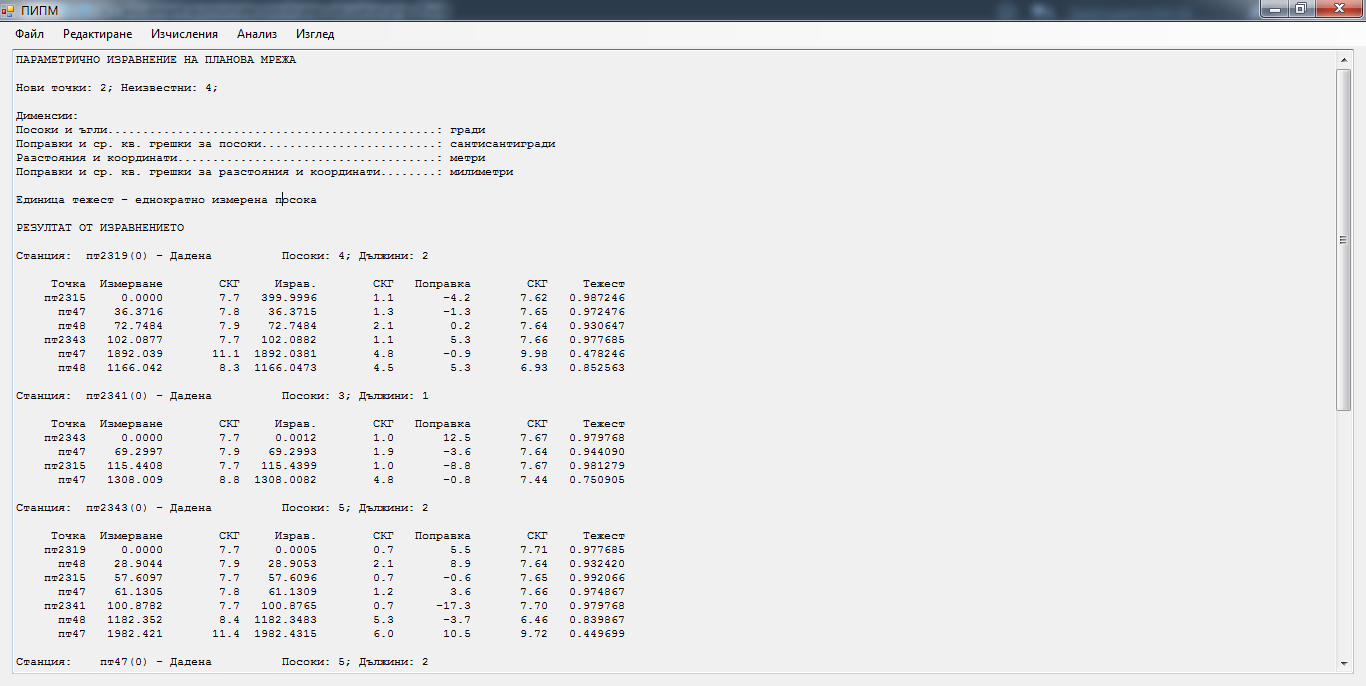
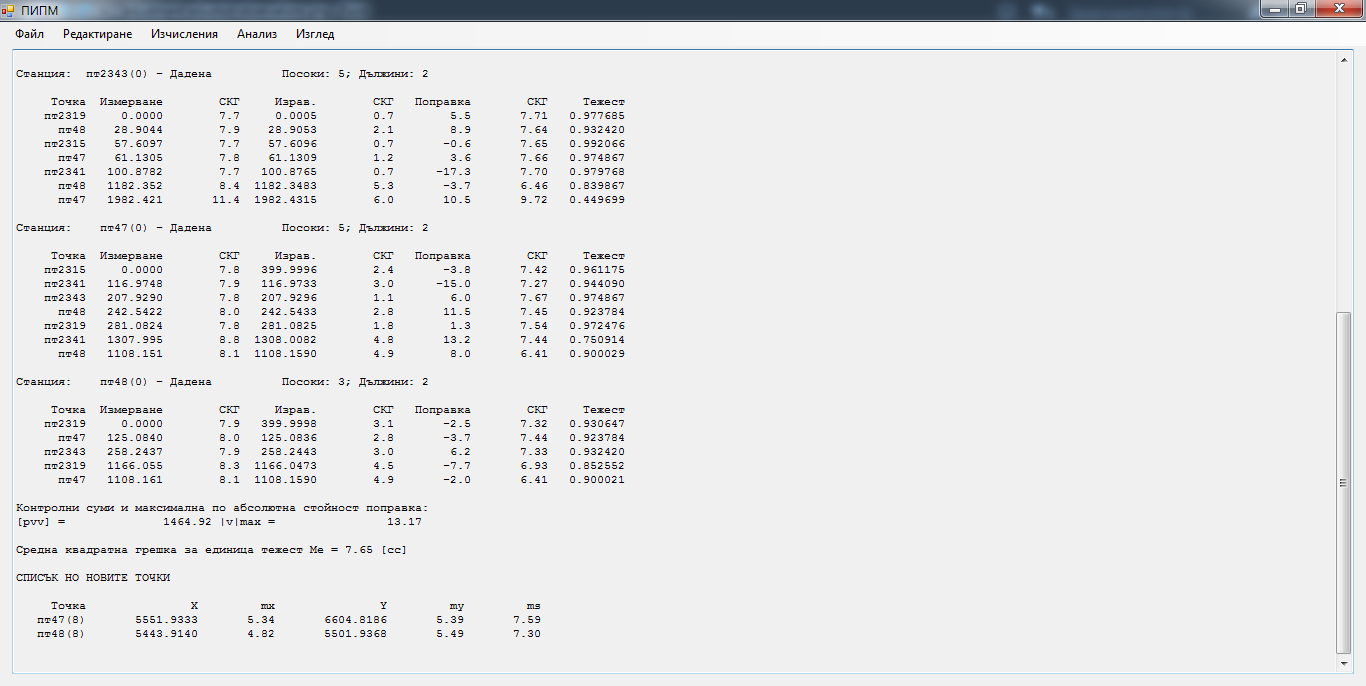
Изравнение на мрежата (измервания и нови точки)
Други
Програма на JavaScript с отворен код за генериране на геодезически измервания във формат DPI за Tplan.
GitHub: https://github.com/Nanich87/Survey-Observations-Generator
Еднозначно решение на линейна засечка
Решението на линейната засечка в геодезията може, най-просто, да се представи като пресичане на две окръжности с радиуси – измерените дължини от новата точка P към две дадени точки A и B, и начало – съответно в точки A и B.
Ако от точка P сме измерили посоки към дадените точки A и B, с помощта на тези посоки можем да определим конфигурацията на триъгълника ABP и съответно да приложим формулите за решаването на линейната засечка. Ако посоките са сортирани по възходящ ред, а разликата между по-голямата и по-малката посока е по малко от 200 гради, то конфигурацията на триъгълника е такава, че точките трябва да участват във формулите обърнато т. е. точка B трябва да участва във формулите като точка A и обратното – точка A трябва да участва като точка B. В противен случай точките не се обръщат. По този начин решението е еднозначно и не се налага търсене на трета дадена точка, към която да е измервана дължина.