Програма за изравнение на планови мрежи
Изравнение на планови мрежи по метода на най-малките квадрати.
Изравнение на засечки – ъглови, линейни, ъглово-линейни, геодезически мрежи, полигони.
Въвеждане на измервания и координати
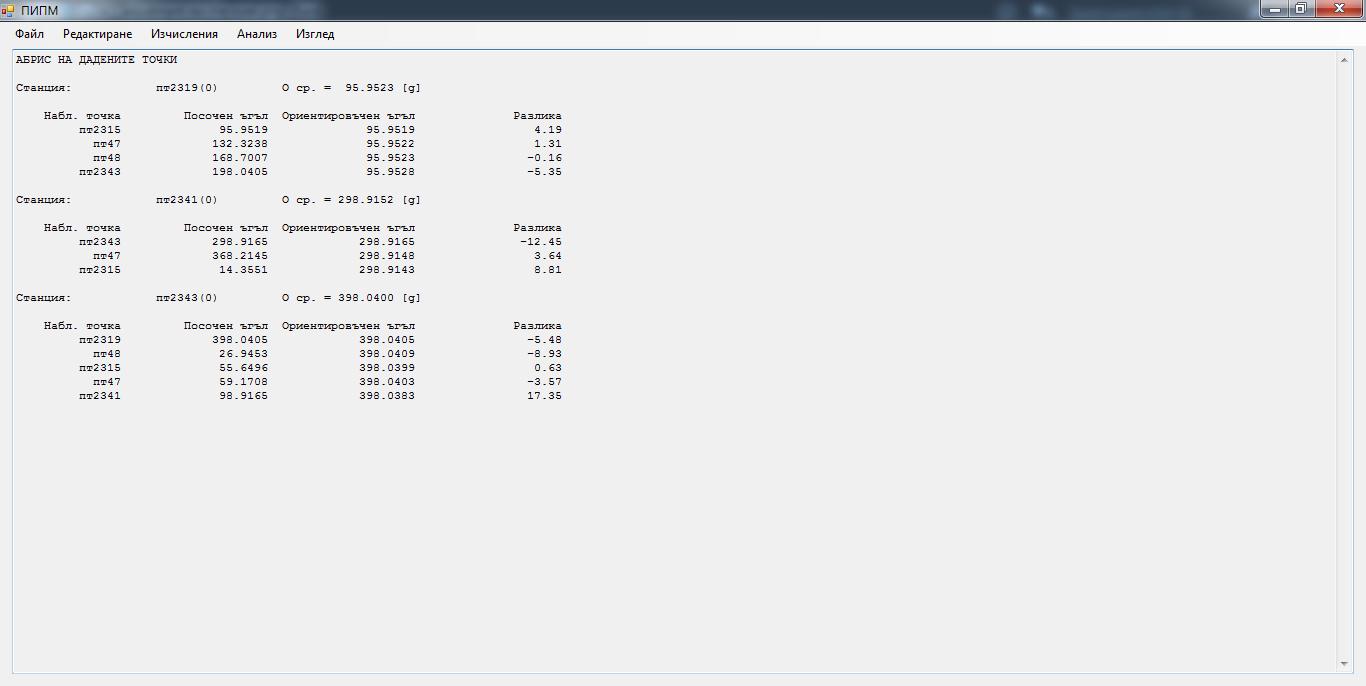
Изчисляване на ориентировъчните ъгли на дадените точки
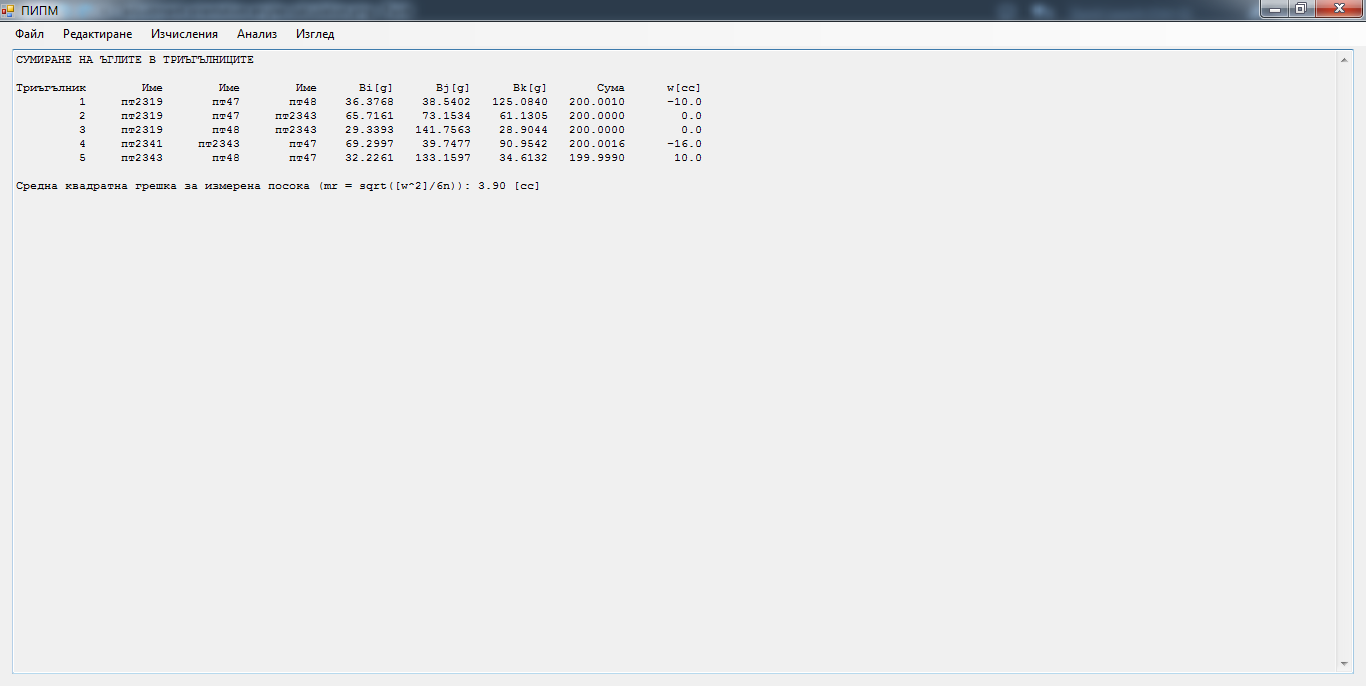
Изчисляване на несъвпаденията в триъгълниците
Изчисляване на приблизителни координати на новите точки
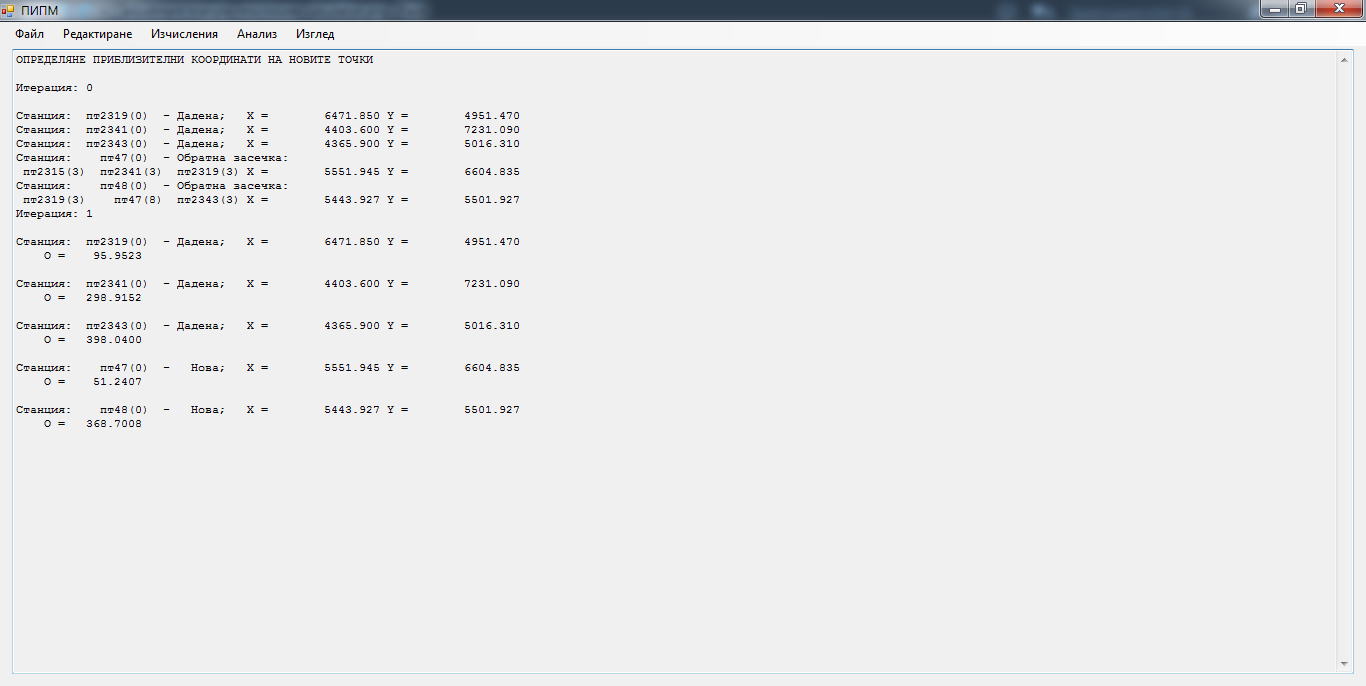
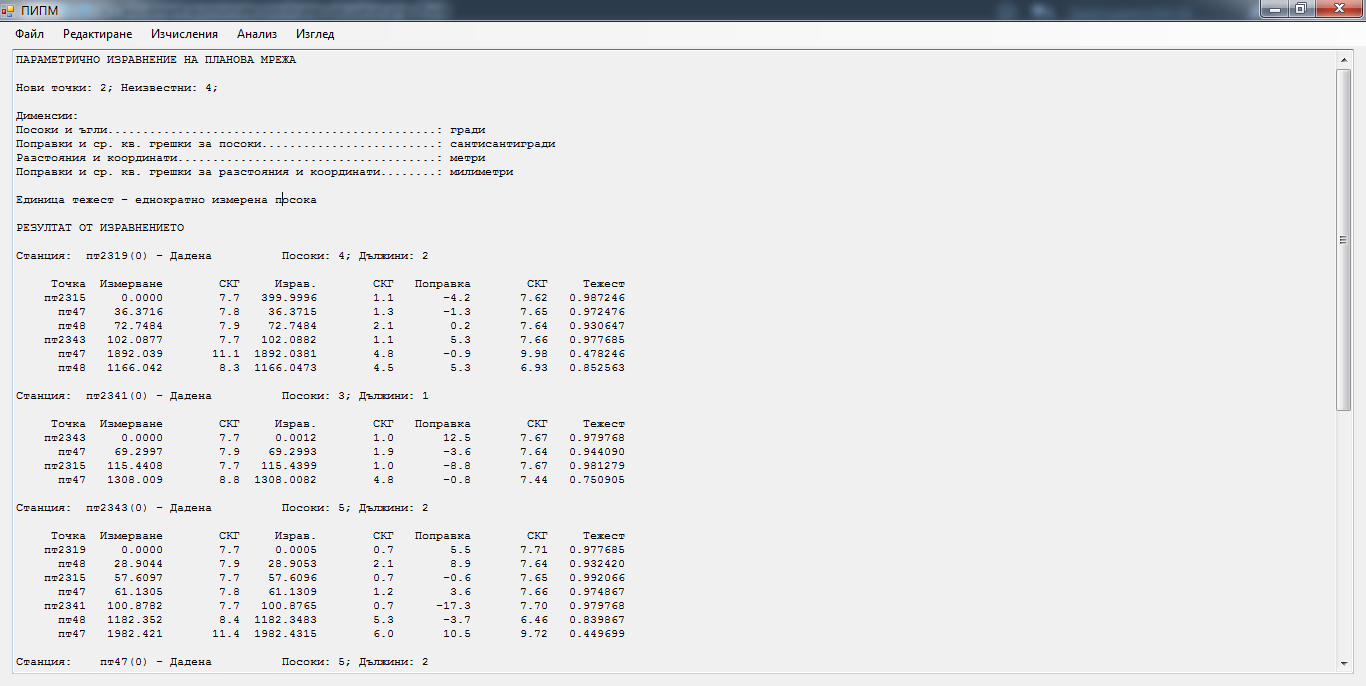
Изравнение на мрежата (измервания и нови точки)
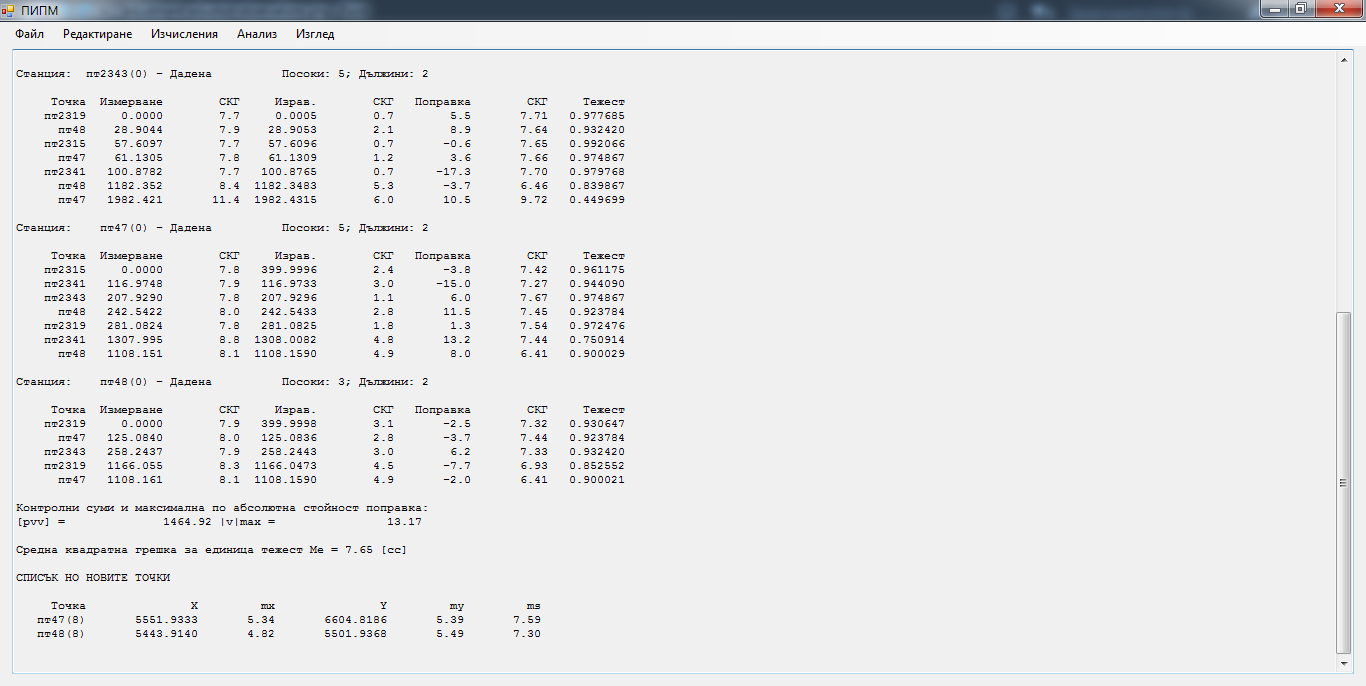
Други